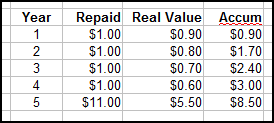
From Professor John Munro's archive page:
c) Why did medieval princes debase their coinages?
i) A commonly given answer is to increase their money supplies in times of precious metal scarcities: i.e. to make a given or reduced quantity of gold and silver go farther, by striking more coins from that metal. But the evidence for such a conscious and deliberate monetary policy to achieve such goals is virtually absent; and debasements cannot be correlated with specific times of coinage or precious metal scarcities.
i) A commonly given answer is to increase their money supplies in times of precious metal scarcities: i.e. to make a given or reduced quantity of gold and silver go farther, by striking more coins from that metal. But the evidence for such a conscious and deliberate monetary policy to achieve such goals is virtually absent; and debasements cannot be correlated with specific times of coinage or precious metal scarcities.
Also, off the top of my head, in times of precious metal scarcities, a given quantity of gold and silver coin will go farther because prices are lower due to the scarcities. So I'm not sure that this "commonly given answer" makes any sense at all.
ii) Most medieval contemporaries thought that the prime motivation for coinage debasement was to increase mint revenues or 'profits' for the prince.
Munro links that thought to this footnote:
See the comment of Nicholas Oresme (ca. 1390), a monetary advisor to King Charles VI of France (and to the dukes of Burgundy): 'I am of the opinion that the main and final cause why the prince pretends to the power of altering the coinage is the profit or gain he can get from it; it would otherwise be vain to make so many and so great changes....
So since medieval times, at least, it has been commonly thought that governments debase currency for their own gain. Otherwise (says Oresme) it would be pointless to debase the currency so frequently.
That's not really a strong argument, Oresme's argument. It's like people today who say "The only explanation is..." and then tell you their favorite explanation. People say that kind of thing all the time, but that doesn't make it a good argument.
iv) The chief object of debasement, when this fiscal motive was present, was to encourage merchants, foreign and domestic, to bring more gold and/or silver bullion to the prince's mints (rather than to foreign mints); and debasements did so by offering such merchants themselves a profit by returning to them more coins of the same face value and current purchasing power (though with a reduced precious metal content) than they would receive from bullion minted by the former coin standard.
People since medieval times thought debasement was common because governments did it for their own profit. Professor Munro presents a different motive: to enhance the profit of the merchants.
This is quite an interesting thought, if the reason for debasement was to enhance the local economy, not just the princely greed.


.png)
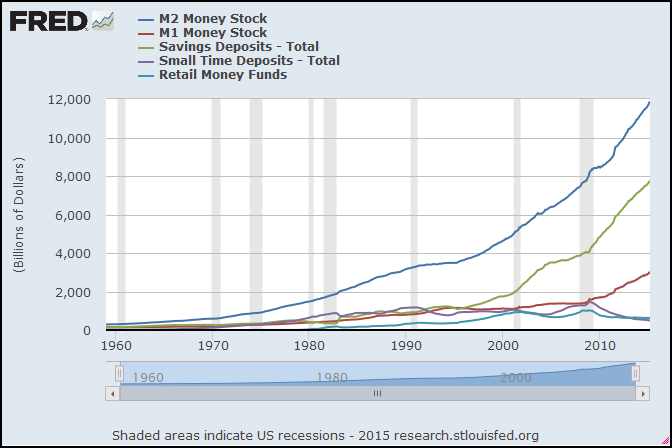
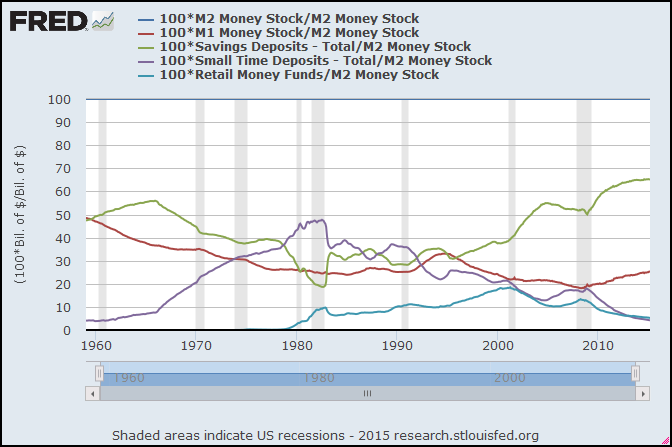
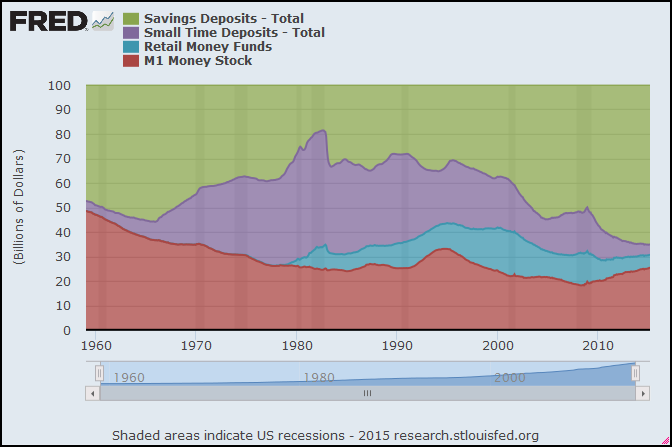




%2Band%2BTotal%2BUS%2BAssets%2B(red).PNG)














.PNG)
.PNG)